With a liminiear approximation can be made from the gradiant. This is done by going the oposite direction.
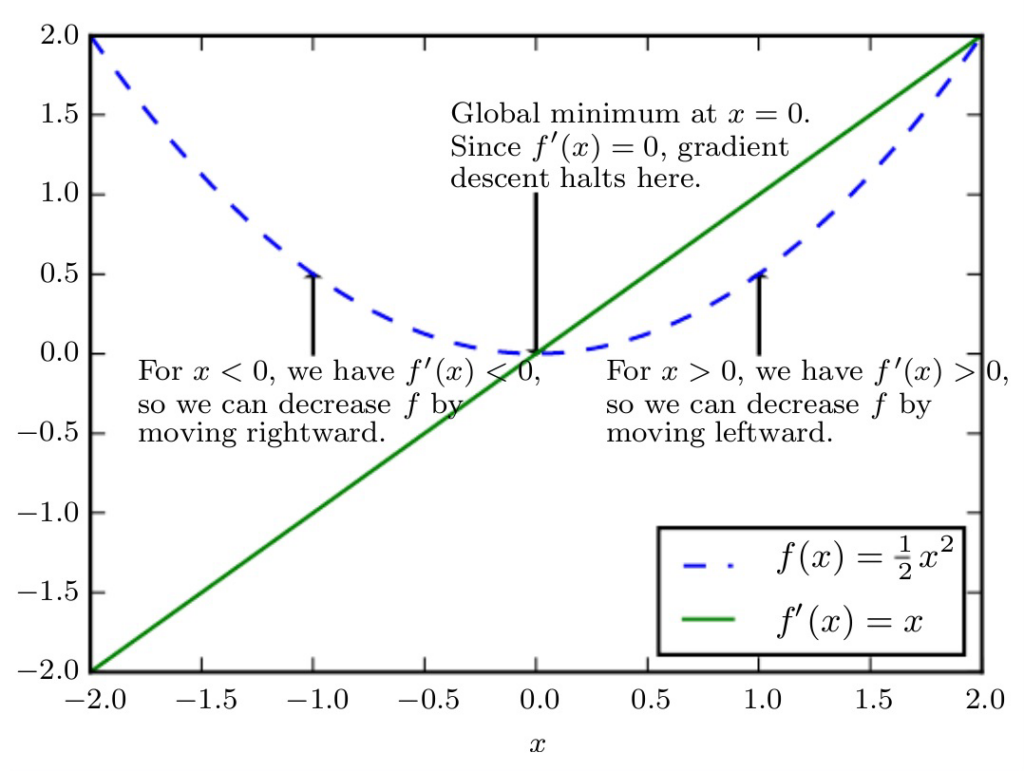
With multiple inputs it is used the same way, but returns an output with weights matching the amount of dimensions of the input.
SGD
SGD is using mini batches. Instead of using all connections to get the most precesise results, batches are used to approximate the result somewhat wore propbably.
From the mini batches an average gradient is calculated and used.
The positive asspect of SGD is that it is faster.
Deep learning specialities
Deep learning needs the same components as machine learning
- Optimization procedure
- Cost function
- Model family
Differences causes non-convex loss.
Problems
- Can end in local minimum
- Can end in local maximum
- Can end at saddle points – The worst point: learning is stopped, and the results are likely not good.
- Learning rate – Big learning rates might have large jumps in results and small learning rates might be slow.
If a particular bad promlem or cliff is encountered, new initialization might be the best solution.
Cliffs and exploding gradients
Cliffs in Neural Network are sudden drops or rices in learning.
Theese can be midigated by implementing a gradient.
Inexact gradients are caused by biace or variance.
About gradients
Gradients must be large and somewhat predictable to guide the learning algorithm.
Functions that saturate (flatten results) undermine gradients.
Negative log-likelihood helps avoid saturation problem for many models. It undoees gradient accidents as far as i understand.
Different optimizers
- SGD
- Standard gradient decent
- utilizes decay, momentum, and Nesterov
- for frequent parameter
- RMSProp
- Root Mean Square Propagation
- utilizes exponentially decaying running average of the squared gradients (similar to momentum)
- decay is usually 0.9.
- Adagrad
- utilizes larger updates for infrequent parameters and smaller updates
- Good for word embeddings with that has infrequent words
- Often has diminising learning rate
- Tries to ease on the diminishing learning rate decay from Adagrad
- Adadelta
- similar to RMSProp
- utilizes root squared parameter updates
- Does not need set learning rate
- Adam
- Adaptive Moment Estimation
- prefers flat minima in the error surface
- Adam is basically RMSProp with momentum
- Adamax
- Same as Adam, but based on the max-norm ^inf.
- Nadam
- Nesterov-accelerated Adaptive Moment Estimation
- Nadam is basically Adam with Nesterov momentum
Choosing a bad optimizer or bad parameters in general, can lead to inefeicent or slow learning.
Batch gradient decent can use fixed learning rate.
SGD jas a source error.
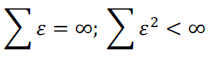
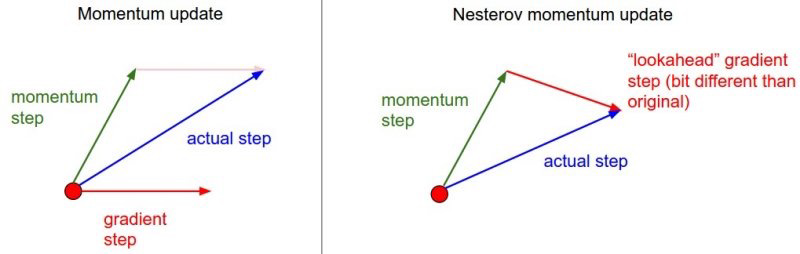
Momentum
Momentum hels accelerea gradientdecent. Usefull when
- Surfaces that curve more steeply in one direction than in another direction
§ Facing high curvature
§ Small but consistent gradients
§ Noisy gradients
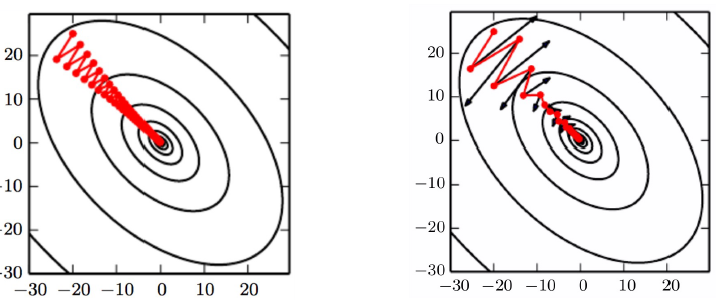
Note: The need for dampening of the oscilation can only be found trhough trial and error.
Momentum introduces velocity, v. It is the direction and speed at which parameters move through parameter
space. Also known as mass in physics.
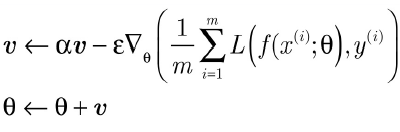
Nesterov Accelerated Gradient
Calculation of gradient if implementet.
Adaptive Learning Rate (ada)
Learning rate for each adaptive parameter.
